Les caractéristiques du marché de l’électricité
Billet avec la liste des articles de cette série
Dans mon dernier billet sur les marchés de l’électricité j’ai mentionné que ceux-ci ont un design bien particulier car l’électricité ne peut être stockée.
La théorie économique n’est cependant pas démunie pour expliquer le fonctionnement de ce type de marché.
La demande
Commençons par la demande. Il y a deux façons de la représenter. En premier on utilise une courbe de la demande dans le temps.
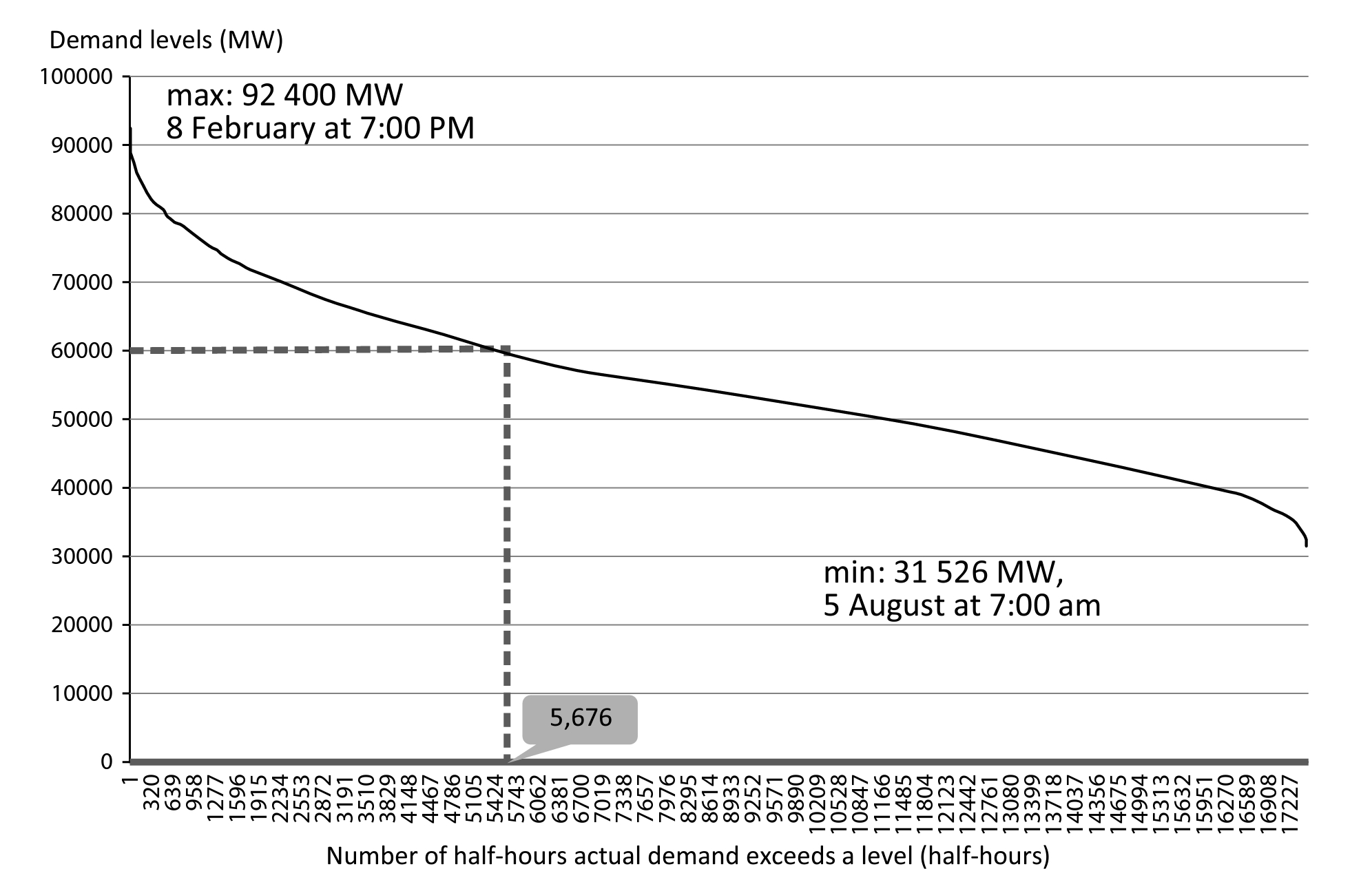
On découpe la demande d’électricité dans une année par tranche d’une demie-heure puis on les classe dans l’ordre décroissant de puissance.
L’exemple pris dans le livre est celui de la France en 2009. On voit que pour les 17 520 demie-heures qui constituent l’année, celle qui a connu la plus forte demande est à 19h le 8 février avec 92 GW et la plus basse est à 7h le 5 août avec 31 GW.
Plusieurs observations:
- On voit que la différence entre les deux extrêmes est quand même grande, on parle d’un triplement entre le minimum et maximum
- Ces demi-heures ne sont pas consécutives, une peut avoir lieu en janvier et la suivante en mars
- Si on prend une puissance sur l’axe des ordonnées, on peut savoir combien de temps dans l’année la demande dépasse ce niveau. Par exemple ici la demande excède 60 GW durant 5676 demie-heures dans l’année. Ceci sera intéressant quand on parlera des sources d’énergie dites « baseload »
- Enfin on constate que la demande dépasse rarement les 90 GW, ce sont ces fameux pics qu’il faut pouvoir gérer alors qu’ils ne durent que peu de temps et ne sont pas fréquents.
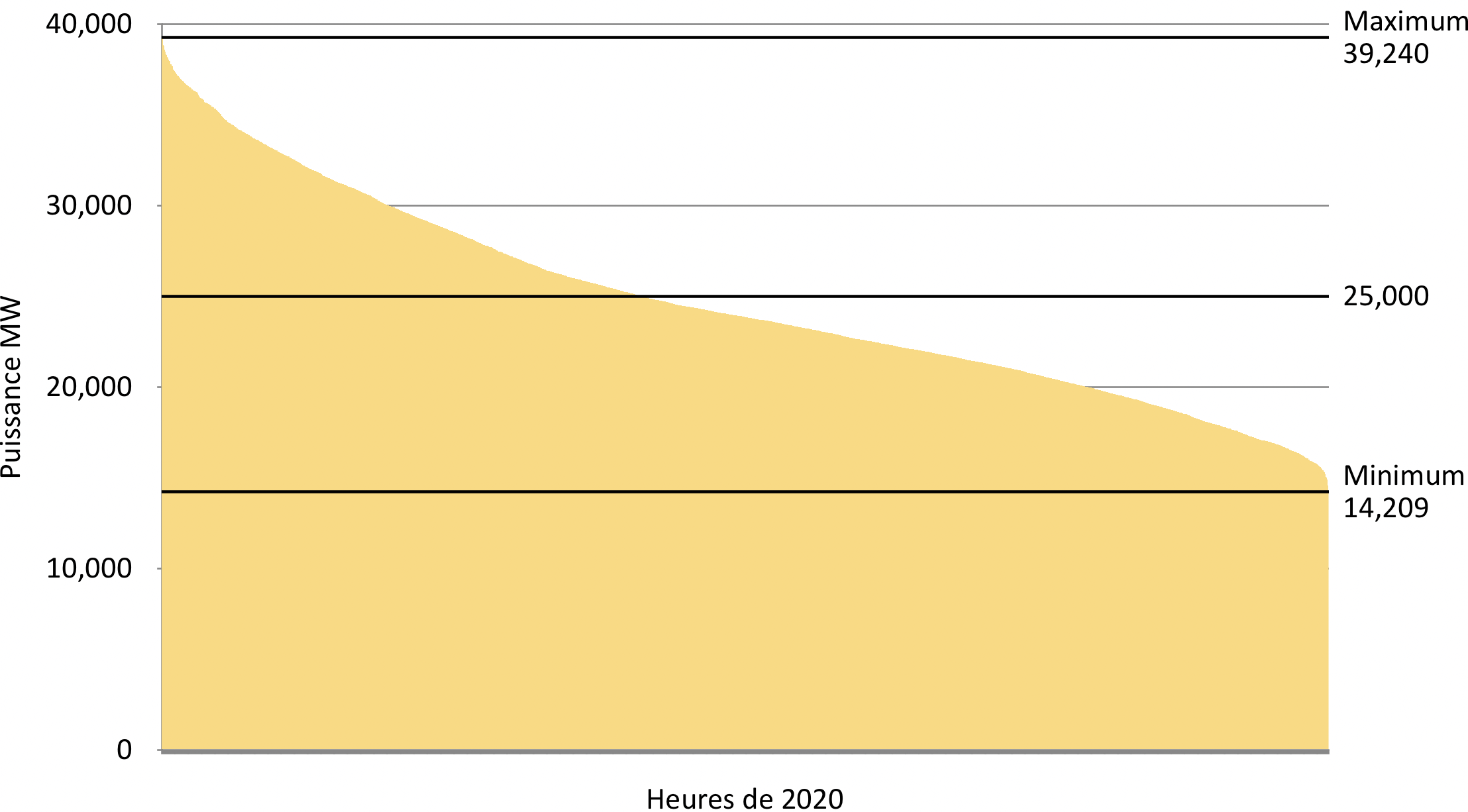
J’ai refait le même graphique pour 2020 à partir des donnés ouvertes de production publiées par Hydro-Québec. Le maximum se situe le 17 janvier à 20h avec un peu plus de 39 GW et le minimum le 31 août à 4h avec 14 GW. Et cette production dépasse 25GW pendant 3 607 heures.
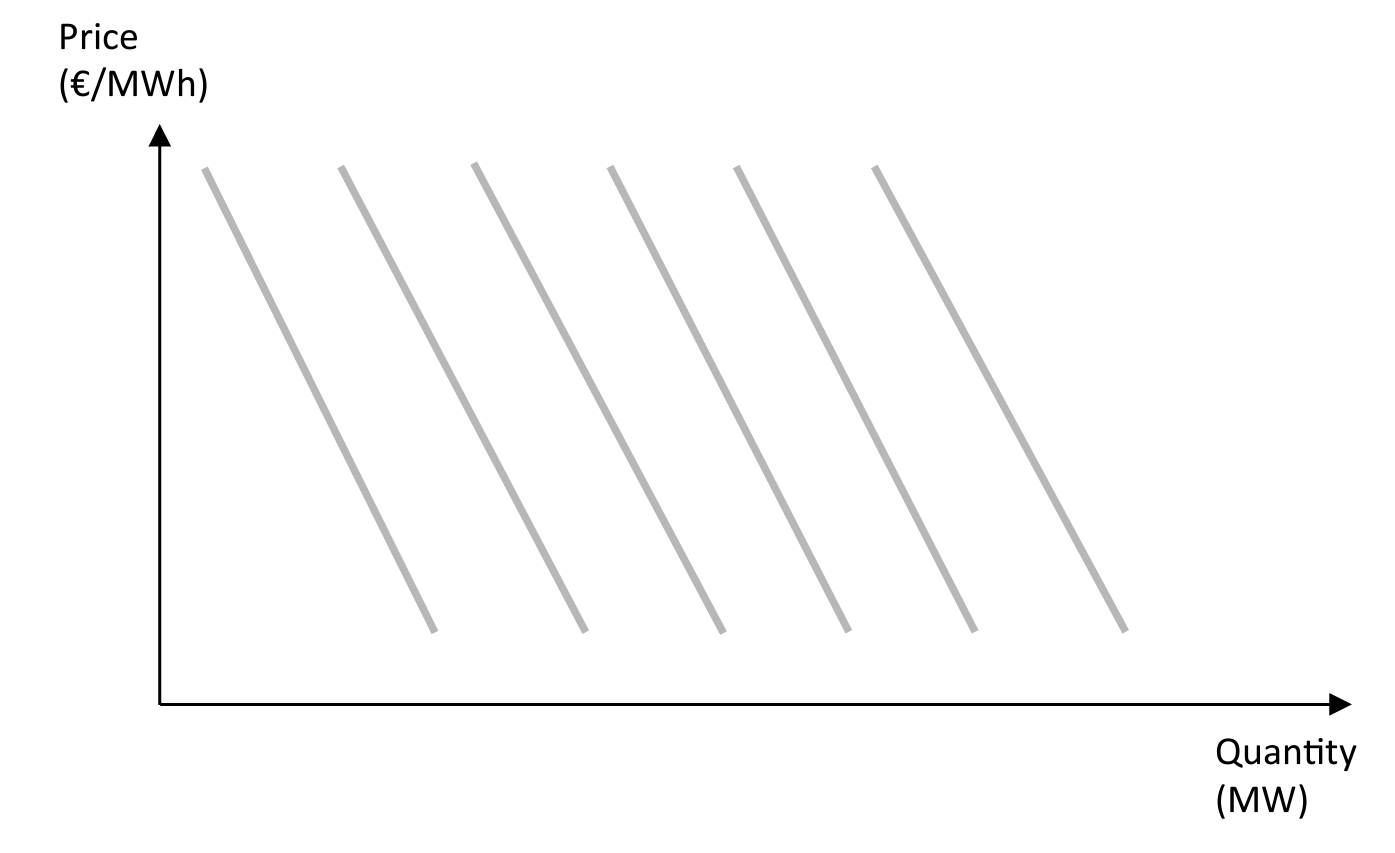
La deuxième représentation est plus classique, elle met en relation le prix avec la demande. C’est la courbe inversée prix-demande. Elle est dite « inversée » car d’habitude la demande est fonction du prix; on verra plus tard que le prix de l’électricité va dépendre de la demande à un moment donné. On a plusieurs courbes qui correspondent aux différentes période de l’année, celle de gauche par exemple correspond à celle d’un matin d’été en France et celle de droite à celle d’un soir d’hiver.
Il existe peu de marchés où la demande peut réagir aux fluctuations du prix en temps réel, la plupart des consommateurs paient un prix fixe et/ou selon la puissance maximale consommée sur une période.
L’offre
Prenons l’hypothèse d’une offre qui est satisfaisante par une seule usine avec une technologie de production unique. Il y a trois paramètres de coût:
- Coût de production horaire variable (c): c’est le coût du fuel pour produire l’électricité, c’est une constante horaire qui se situe environ entre 20 et 100 euros / MWh selon le cours du pétrole mais qui est presque nul pour le solaire et l’éolien
- Coût de production horaire fixe (r): c’est le coût de dépréciation, retour sur investissement, taxes, opérations et maintenances. Appelé aussi « capacity cost »; on divise ce coût annuel par le nombre d’heures (8760) pour avoir le coût horaire
Une des corollaires est un rendement constant à l’échelle. Si l’usine de production a une capacité de K MW, elle ne peut pas produire une quantité Q tel que Q > K et si Q < K le coût de production horaire total sera rK + cQ. Prenons un exemple.
Si nous avons trois usines usines de même technologie, deux usines de 200 MW et une autre de 400 MW. Avec un coût variable c de 10 et un coût fixe r de 2.
Si on doit produire 400 MWh. Le coût total horaire des deux premières représentent (200 * 2) + (10*200) = 2 400 par usine soit 4 800 au total. Tandis que l’usine de 400 MW aura un coût de (400 * 2) + (10 * 400) soit le même montant de 4 800. Produire les 400 MWh a le même coût quelque soit l’échelle de production.
La rencontre de l’offre et la demande
Le problème à résoudre est de trouver un prix et une capacité de production qui permettent de répondre à la demande sachant que celle-ci varie selon le moment de la journée et les saisons.
De plus, l’électricité ne se stocke pas encore. On ne peut pas prendre, à grande échelle, un surplus de production à un moment donné pour satisfaire la demande à un autre. On peut le faire à petite échelle avec des panneaux solaires et une batterie en stockant l’énergie générée en milieu de journée pour l’utiliser le soir quand ces panneaux ne fournissent plus d’électricité. Mais nous n’avons pas encore de solution viable pour du stockage à grande échelle et sur plusieurs mois.
Les auteurs du manuel rapprochent ce problème à celui des avions ou des hôtels où la demande varie face à un moyen de « production » qui ne peut pas se mettre à l’échelle facilement. Autrement dit une chambre d’hôtel non occupée ou un siège non vendu sont « perdus » quand la nuit tombe ou l’avion décolle.
Le prochain billet décrira une première solution à ce problème.
Billet avec la liste des articles de cette série